正切函数的性质：

      1、定义域：{x|x≠(π/2)+kπ,k∈Z}。
      2、值域：实数集R。
      3、奇偶性：奇函数。
      4、单调性：在区间(-π/2+kπ,π/2+kπ)，（k∈Z）上是增函数。
      5、周期性：最小正周期π（可用T=π/|ω|来求）。
      6、最值：无最大值与最小值。
      7、零点：kπ,k∈Z。
      8、对称性：无轴对称：无对称轴中心对称：关于点(kπ/2+π/2,0)对称（k∈Z）。
      9、奇偶性：由tan（-x）=-tan（x），知正切函数是奇函数，它的图象关于原点呈中心对称。
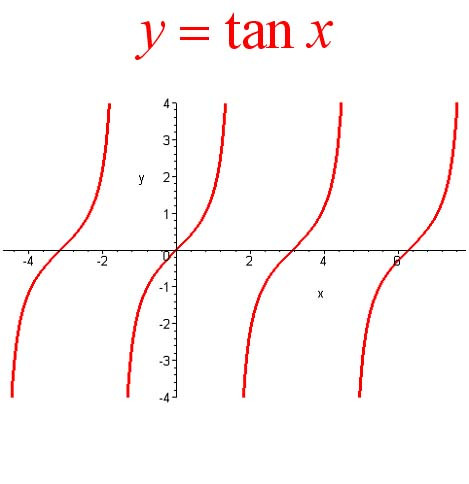
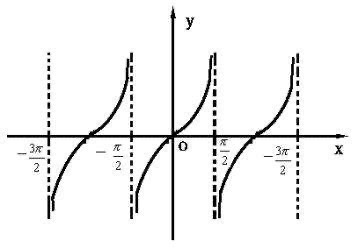
      10、图像（如图所示）实际上，正切曲线除了原点是它的对称中心以外,所有x=(n/2)π （n∈Z） 都是它的对称中心。

       在平面三角形中，正切定理说明任意两条边的和除以第一条边减第二条边的差所得的商等于这两条边的对角的和的一半的正切除以第一条边对角减第二条边对角的差的一半的正切所得的商。
       法兰西斯·韦达(François Viète)曾在他对三角法研究的第一本著作《应用于三角形的数学法则》中提出正切定理。现代的中学课本已经甚少提及，例如由于中华人民共和国曾经对前苏联和其教育学的批判，在1966年至1977年间曾经将正切定理删除出中学数学教材。不过在没有计算机的辅助求解三角形时，这定理可比余弦定理更容易利用对数来运算投影等问题。

       正切定理： (a + b) / (a - b) = tan((α+β)/2) / tan((α-β)/2)
       tanA·tanB·tan(A+B)+tanA+tanB-tan(A+B)=0
       高等代数中三角函数的指数表示(由泰勒级数易得)：
       sinx=[e^(ix)-e^(-ix)]/(2i)
       cosx=[e^(ix)+e^(-ix)]/2
       tanx=[e^(ix)-e^(-ix)]/[ie^(ix)+ie^(-ix)]
       tanA·tanB=1