对称轴：关于直线x=(π/2)+kπ，k∈Z对称。正弦函数是三角函数的一种。对于任意一个实数x都对应着唯一的角，而这个角又对应着唯一确定的正弦值sinx，这样，对于任意一个实数x都有唯一确定的值sinx与它对应，按照这个对应法则所建立的函数，表示为y=sinx，叫做正弦函数。

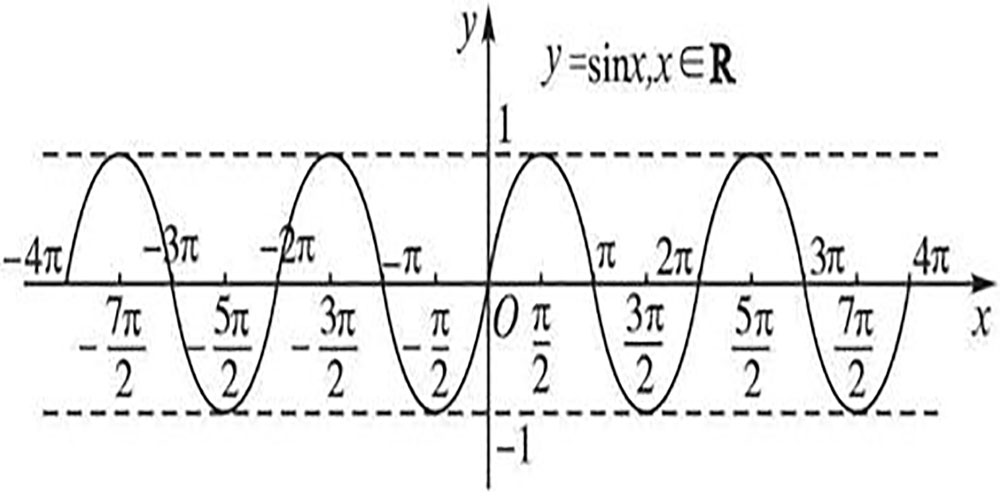
　　正弦函数基本性质

　　1、定义域

　　实数集R，可扩展到复数集C

　   2、值域

　　[-1，1]（正弦函数有界性的体现）

　　最值和零点

　　①最大值：当x=2kπ+(π/2)，k∈Z时，y(max)=1

　　②最小值：当x=2kπ+(3π/2)，k∈Z时，y(min)=-1

　　零值点：(kπ，0)，k∈Z

　　3、对称性

　　1)对称轴：关于直线x=(π/2)+kπ，k∈Z对称

　　2)中心对称：关于点(kπ,0)，k∈Z对称

　   4、周期性

　　最小正周期：2π

　　5、奇偶性

　　奇函数(其图象关于原点对称)

　   6、单调性

　　在[-(π/2)+2kπ,(π/2)+2kπ]，k∈Z上是增函数

　　在[(π/2)+2kπ,(3π/2)+2kπ]，k∈Z上是减函数